Joshua Hintz versus the Collatz problem
Joshua Hintz
2022-12-22
1 Prologue (roughly translated from German)
Johannes: Hey look at me. I have a website.
Joshua: Thats a waste of internet. Why are there no advertisements?
Johannes: Its my site. I can upload what I want. Which is not advertisements.
Joshua: You know how I have been working on solving this famous unsolved mathematical problem?
Johannes: The Collatz problem. Yes, we have all been making fun of that.
Joshua: You can upload my findings. I would send them to you.
Johannes: Emm cool. Just send it to me in some text format, can you do that? Ideally markdown or HTML.
Joshua: You mean Word? I wrote it in Word.
Johannes: Sry m8, it has to be a text format or I can’t work with it…
Joshua: I know excactly how to do it. Wait one moment.
Johannes: .. You are gonna do something stupid, right?
2 The Collatz problem
Joshua Hintz
Erstellungsdatum: 3. März 2022
Aktualisierungsdatum: 06.12.2022
3 Einleitung
3.1 Collatz-Problem
Man Wähle ein beliebiges \(c_0{\in}N\)
Collatz-Regel:
Regel A: \(c_n\) ist gerade: \(c_{n+1}=\frac{c_n} 2\)
Regel B: \(c_n\) ist ungerade: \(c_{n+1}=3\ast c_n+1\)
Bsp. \(c_0=3\):
\[\begin{equation*} 3\rightarrow 10\rightarrow 5\rightarrow 16\rightarrow 8\rightarrow 4\rightarrow 2\rightarrow 1\rightarrow 4\rightarrow 2\rightarrow 1\rightarrow 4{\cdots} \end{equation*}\] Die Frage des Collatz-Problems liegt darin, ob jeder Startwert c in der Schleife \(4\rightarrow 2\rightarrow 1\rightarrow 4\) endet.
4 Binärsystem-Zahlenbaum
Um zu beweisen, dass alle Zahlen beim Anwenden der Collatz-Regel auf 1 enden, kann die Collatz-Regel auch R"uckwerts betrachtet werden, mit eins als Startwert. Wenn nur Regel A angewendet wird entsteht: \(1\rightarrow 2\rightarrow 4\rightarrow 8\rightarrow 16\rightarrow ...\) .
Damit enden alle Zahlen aus \(2^x\) auf 1. \(x{\in}N\)
Im Binärsystem ist \(2^x=100000{\cdots}\) , mit x Nuller nach der 1.
Jede Gerade Zahl muss nach Regel A so lange durch 2 geteilt werden, bis diese auf eine ungerade zahl liegt. Im Binärsystem erfolgt dies durch das K"urzen der Nuller am Ende der Zahl.
Bsp.: \(1100\rightarrow 11\). (Vergleich Dezimalsystem: \(12\rightarrow 6\rightarrow 3\))
Deswegen werden im Folgenden die Regel A damit erf"ullt, dass die 0 am Ende der Zahl im Binärsystem ignoriert werden.
Im Binärsystem kann die Zahl 1000{} (x Anzahl Nuller) durch befolgen der Collatzregeln gebaut werden:
\(1000{\cdots}-1=\frac{11111{\cdots}}{11}=101010101{\cdots}.\) . F"ur x gerade Anzahl an 0 bzw. 1. Ungerade Anzahl ist nicht durch 11 teilbar.
Eine weitere Methode, um die Zahl 1000 {} zu bilden ist Folgende:
10000 {} 00000
(Anfangszahl) 1 -\(\textgreater\) Regel B -\(\textgreater\) 100. Erste Stelle 0 richtig, zweite Stelle 0 richtig, dritte Stelle 1 falsch -\(\textgreater\)
101 -\(\textgreater\) Regel B -\(\textgreater\) 10000. Erste bis vierte Stelle richtig. 5 Stelle falsch -\(\textgreater\)
[Warning: Draw object ignored] 10101 -\(\textgreater\) Regel B -\(\textgreater\) 1000000. Erste bis sechste Stelle richtig. 7 Stelle falsch -\(\textgreater\)
\(\cdots\)
10101 \(\cdots\) 010101.
Diese Methode funktioniert deswegen, da bei Regel B mit 11, eine ungerade Zahl, multipliziert wird. Durch das Ergänzen der 1 an der ersten falschen Stelle (von rechts nach links betrachtet) wird der Zahlenwert 1, nach der Anwendung der Regel B, auf 0 geändert:
\[\begin{equation*} 101\ast 11+1=100\ast 11+1\ast 11+1=1100+100=10000 \end{equation*}\] Dieser 1 Wert, sorgt daf"ur, dass nun der gew"unschte 0 Wert nach der Anwendung der Regel B an der Stelle steht. Dabei ändert sich zwar die nachfolgenden Stellen beim Ergebnis, jedoch k"onnen diese ebenfalls Schritt f"ur Schritt korrigiert werden. Die Erläuterung bedarf noch weiterer Erklärung, welche sich jedoch bei den folgenden Betrachtungen er"ubrigen sollten.
Als nächsten soll die Zahl bzw. das Zahlenmuster 1010101{} gebildet werden. Da Regel A Angewendet wird, darf die Zahl 1010101{} beliebig viele Nuller am Ende haben, da durch das wegefallen der Nuller wieder das Zahlenmuster 1010101 entsteht.
{}1010101010101010101000000{} 000000
1
101
10101 {} 10101
Durch die Nuller am Anfang entsteht das Zahlenmuster 1010101{} am Anfang der Zahl wieder. Die Nuller am Anfang k"onnen durch zwei Fälle zusammengefasst werden:
{} 1010101010 und {} 10101010100
Erster Fall:
..1010101010101010
1 -\(\textgreater\) Regel B: 100. Erste Stelle 0 richtig. Zweite Stelle 0 falsch:
11 -\(\textgreater\) 001010. Ersten 6 Stellen richtig. 7 Stelle falsch.
100011 -\(\textgreater\) \(\cdots\)
1100011 -\(\textgreater\) \(\cdots\)
11100011 -\(\textgreater\) \(\cdots\)
{} 0011100011100011
Um auf das Zahlenmuster 1010101… zu kommen, muss die Zahl vor der Anwendung der Regel B (und Regel A) das Zahlenmuster 111000111000111000111{} . Dabei wird folgendes ebenfalls ersichtlich:
11 -\(\textgreater\) 101; 11100011 -\(\textgreater\) 101010101;
100011 -\(\textgreater\) 1101; 1100011 -\(\textgreater\) 100101;
Das Zahlenmuster 111000111\(\cdots\) kann folglich nicht an beliebigen Stellen abgebrochen werden.
Zunächst wird noch Fall 2 betrachtet:
{}10101010100
1 -\(\textgreater\)
\(\cdots\).
{}10001110001.
Beide Fälle sind Teil desselben Zahlenmuster, jedoch ist der Anfang des Zahlmuster unterschiedlich. Die Zahlenmuster k"onnen folglich nur an Bestimmten Stellen Anfangen und Enden.
Was bei weiteren Betrachtungen ersichtlich wird, ist dass die ersten zwei Stellen der Zahl aus dem Zahlenmuster nicht aus dem Muster kommen muss. Das liegt an daran, dass auf die erste Stell, durch die Anwendung der Regel B, noch eine 1 addiert wird.
Wird dieser Methode weiterhin gefolgt, entstehen weitere Zahlenmuster. Um zu zeigen, dass alle Zahlen, aus diesem Zahlenmustern kommen und damit folglich auf 1 Enden, m"ussen die Zahlenmuster verstanden werden.
5 Zahlenmuster Verständnis
Anstatt auf 10000 {} die Regel B anzuwenden, wird auf 1,0000{} die Regel B angewendet. (Dezimalsystem:) wird 1,000… , durch die Umkehranwendung der Regel B, durch 3 geteilt, ist das Ergebnis \(\frac 1 3\). Im Binärsystem ist die Dezimalzahl \(\frac 1 3\) die Zahl 0,01010101{} , welches mit den Zahlenmuster 1010101.. zu vergleichen ist. Die +1 aus der Regel B sorgt daf"ur, dass das Zahlenmuster 1010101{} nicht unendlich fortgesetzt wird, sondern an bestimmten Stellen abgebrochen werden kann (F"ur dieses Zahlenmuster, an jeder Stelle).
F"ur die weiteren Zahlenmuster gilt (links Dezimalsystem, rechts Binärsystem):
\[\begin{equation*} \frac 1 9=0,0001110001110001110{\cdots} \end{equation*}\] \[\begin{equation*} \frac 1{27}=0,00001001011110110100001001011{\cdots} \end{equation*}\] {}
Um die Zahlenmuster zu verstehen, wird \(3^x\) im Binärsystem betrachtet:
1
11
1001
11011
1010001
11110011
{}
Die Zahlen folgen der Logik \(3^x\). Beim Betrachten der Zahlen ist diese Logik jedoch nicht ersichtlich.
Im Binärsystem wird \(11\ast 11\) wie folgt gerechnet:
\[\begin{equation*} 11\ast 11=? \end{equation*}\] \[\begin{equation*} 11 \end{equation*}\] \[\begin{equation*} +110 \end{equation*}\] \[\begin{equation*} =1001 \end{equation*}\] Anstatt die zweite Stelle aufzurunden, werden die Zahlenwerte stehen gelassen:
\[\begin{equation*} 11\ast 11=? \end{equation*}\] \[\begin{equation*} 11 \end{equation*}\] \[\begin{equation*} +110 \end{equation*}\] \[\begin{equation*} =121 \end{equation*}\] Bei dieser Methode sind die Zahlen immer noch auf den Stellen der jeweiligen 2-Potenz:
Tabelle 1.0
Durch diese Methode entsteht das Pascalsche Dreieck. Das Pascalsche Dreieck kann auch r"uckwärts angewendet werden:
Tabelle 1.1
Die umgekehrte Anwendung des Pascalschen Dreiecks nähern sich den Zahlenmustern aus dem Binärsystem an:
Bsp.: 1 -2 3 {}-4 5 {}-6 7 {}-8 9 {}-10 11 {}-12 …
Tabelle 1.2
Damit alle Zahlen im Collatz-Problem auf 1 enden, m"ussen alle Zahlen teil des r"uckwärts angewendeten Pascalschen Dreieckes sein. Da die Zahlmuster nicht an beliebigen Stellen anfangen und enden durften, m"ussen die Anfänge und Enden im Pascalschen Dreieck verstanden werden.
6 Kombinationen aus verschiedenen Pascalschen Dreiecken
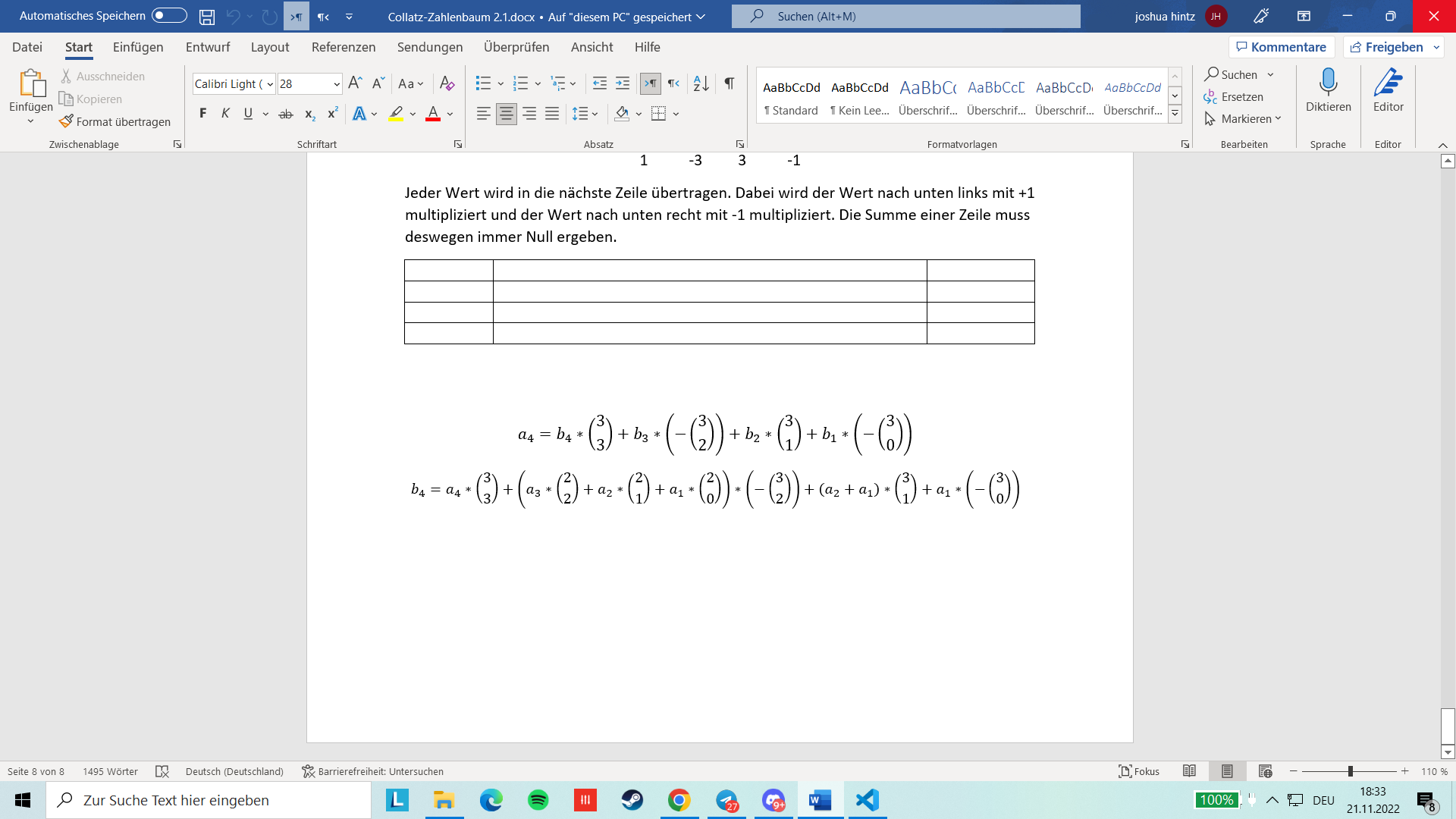
Anstatt direkt die eins zu subtrahieren, aus der Umkehrten Regel {}dividiere durch drei und subtrahiere eins``, wird diese nicht verrechnet. Des Weiteren ist es m"oglich die Zahlenwerte aus dem Pascalschen Dreieck als Binärkoeffizienten zu schreiben.
Die BS-Struktur ist dabei so aufgebaut, dass wenn der Wert \(\left(\genfrac{}{}{0pt}{0}00\right)\) subtrahiert wird, dieser den Potenzwert von \(2^{-1}\) im BS besitzt. Damit ergibt sich die restliche Verteilung der Potenzen.
Bsp. 17:
Damit ergibt sich Folgende Summe:
\[\begin{equation*} 17=\sum _0^6\left(\genfrac{}{}{0pt}{0}{n+2}2\right)\ast 2^{6-n}\ast \left(-1\right)^n+\sum _0^2\left(\genfrac{}{}{0pt}{0}{n+2}2\right)\ast 2^{2-n}\left(-1\right)^n+\sum _0^0\left(\genfrac{}{}{0pt}{0}{n+1}1\right)\ast 2^n\left(-1\right)^n+\sum _{n=0}^{{\infty}}\left(-\left(\genfrac{}{}{0pt}{0}{n+9}2\right)+\left(\genfrac{}{}{0pt}{0}{n+5}2\right)+\left(\genfrac{}{}{0pt}{0}{n+2}1\right)-\left(\genfrac{}{}{0pt}{0}n0\right)\right)\ast 2^{-\left(n+1\right)}\ast \left(-1\right)^n \end{equation*}\] Im Folgenden wird das Bsp der Zahl 17 betrachtet. Einzelne Zahlenwerte werden Zusammengefasst.
\[\begin{equation*} \left(-\left(\genfrac{}{}{0pt}{0}{n+9}2\right)+\left(\genfrac{}{}{0pt}{0}{n+5}2\right)+\left(\genfrac{}{}{0pt}{0}{n+2}1\right)-\left(\genfrac{}{}{0pt}{0}n0\right)\right)=k_n \end{equation*}\] Zur Vereinfachung der rot markierten Summe wird das Pascalsche Dreieck mit negativer Erweiterung betrachtet:
Folglich gilt, da auch das Pascalsche Dreieck mit Binärkoeffizienten dargestellt werden kann:
\[\begin{equation*} 3^{-(x+1)}=\sum _{n=0}^{{\infty}}\left(\genfrac{}{}{0pt}{0}{n+x}x\right)\ast 2^{-\left(n+1+x\right)}\ast \left(-1\right)^n \end{equation*}\] Der einzige Zahlenwert der bei \(2^{-1}\) einen Wert besitzt ist \(3^{-1}\). Dieser Wert ist bei der Zahl 17 \(a_1\). Somit ergibt sich:
\[\begin{equation*} b_1\ast 3^{-1}=a_1\ast \left(\genfrac{}{}{0pt}{0}00\right)\ast 3^{-1}=a_1\ast \left(\genfrac{}{}{0pt}{0}00\right)\ast \sum _{n=0}^{{\infty}}\left(\genfrac{}{}{0pt}{0}n0\right)\ast 2^{-\left(n+1\right)}\ast \left(-1\right)^n \end{equation*}\] Die Zahl 17 kann somit wie folgt dargestellt werden:
\[\begin{equation*} 17=c+a_1\ast 3^{-1}+\sum _{n=0}^{{\infty}}(k?_n-a_1\ast \left(\genfrac{}{}{0pt}{0}n0\right))\ast 2^{-\left(n+1\right)}\ast (-1)^n \end{equation*}\] In der Tabelle ist der einzige Zahlenwert der bei \(2^{-2}\) einen Wert besitzt ist \(3^{-1}\) und \(3^{-2}\). Damit gilt
\[\begin{equation*} a_2=b_2\ast \left(\genfrac{}{}{0pt}{0}11\right)+b_1\ast \left(-\left(\genfrac{}{}{0pt}{0}10\right)\right) \end{equation*}\] \[\begin{equation*} b_2=a_2+b_1\ast \left(\genfrac{}{}{0pt}{0}10\right)=a_2+a_1 \end{equation*}\] Somit gilt f"ur \(2^{-n}\):
\[\begin{equation*} a_n=\sum _{t=0}^{n-1}b_{n-t}\ast \left(\genfrac{}{}{0pt}{0}{n-1}t\right)\ast \left(-1\right)^{n-t+1} \end{equation*}\] Es gilt:
\[\begin{equation*} b_n=\sum _{t=0}^{n-1}a_{n-t}\ast \left(\genfrac{}{}{0pt}{0}{n-1}t\right) \end{equation*}\] Damit dies der Fall ist muss gelten:
\[\begin{equation*} A=\left(\begin{matrix}\begin{matrix}\left(\genfrac{}{}{0pt}{0}00\right)&0\\-\left(\genfrac{}{}{0pt}{0}11\right)&\left(\genfrac{}{}{0pt}{0}10\right)\end{matrix}&\begin{matrix}0&0\\0&0\end{matrix}&\begin{matrix}0&{\cdots}\\0&{\cdots}\end{matrix}\\\begin{matrix}\left(\genfrac{}{}{0pt}{0}22\right)&-\left(\genfrac{}{}{0pt}{0}21\right)\\-\left(\genfrac{}{}{0pt}{0}33\right)&\left(\genfrac{}{}{0pt}{0}32\right)\end{matrix}&\begin{matrix}\left(\genfrac{}{}{0pt}{0}20\right)&0\\-\left(\genfrac{}{}{0pt}{0}31\right)&\left(\genfrac{}{}{0pt}{0}30\right)\end{matrix}&\begin{matrix}0&{\cdots}\\0&{\cdots}\end{matrix}\\\begin{matrix}\left(\genfrac{}{}{0pt}{0}44\right)&-\left(\genfrac{}{}{0pt}{0}43\right)\\{\vdots}&{\vdots}\end{matrix}&\begin{matrix}\left(\genfrac{}{}{0pt}{0}42\right)&-\left(\genfrac{}{}{0pt}{0}41\right)\\{\vdots}&{\vdots}\end{matrix}&\begin{matrix}\left(\genfrac{}{}{0pt}{0}40\right)&{\cdots}\\{\vdots}&{\ddots}\end{matrix}\end{matrix}\right) \end{equation*}\] \[\begin{equation*} B=\left(\begin{matrix}\begin{matrix}\left(\genfrac{}{}{0pt}{0}00\right)&0\\\left(\genfrac{}{}{0pt}{0}11\right)&\left(\genfrac{}{}{0pt}{0}10\right)\end{matrix}&\begin{matrix}0&0\\0&0\end{matrix}&\begin{matrix}0&{\cdots}\\0&{\cdots}\end{matrix}\\\begin{matrix}\left(\genfrac{}{}{0pt}{0}22\right)&\left(\genfrac{}{}{0pt}{0}21\right)\\\left(\genfrac{}{}{0pt}{0}33\right)&\left(\genfrac{}{}{0pt}{0}32\right)\end{matrix}&\begin{matrix}\left(\genfrac{}{}{0pt}{0}20\right)&0\\\left(\genfrac{}{}{0pt}{0}31\right)&\left(\genfrac{}{}{0pt}{0}30\right)\end{matrix}&\begin{matrix}0&{\cdots}\\0&{\cdots}\end{matrix}\\\begin{matrix}\left(\genfrac{}{}{0pt}{0}44\right)&\left(\genfrac{}{}{0pt}{0}43\right)\\{\vdots}&{\vdots}\end{matrix}&\begin{matrix}\left(\genfrac{}{}{0pt}{0}42\right)&\left(\genfrac{}{}{0pt}{0}41\right)\\{\vdots}&{\vdots}\end{matrix}&\begin{matrix}\left(\genfrac{}{}{0pt}{0}40\right)&{\dots}\\{\vdots}&{\ddots}\end{matrix}\end{matrix}\right) \end{equation*}\] \[\begin{equation*} A\ast B=\left(\begin{matrix}\begin{matrix}1&0\\0&1\end{matrix}&\begin{matrix}0&0\\0&0\end{matrix}&\begin{matrix}0&{\dots}\\0&{\dots}\end{matrix}\\\begin{matrix}0&0\\0&0\end{matrix}&\begin{matrix}1&0\\0&1\end{matrix}&\begin{matrix}0&{\dots}\\0&{\dots}\end{matrix}\\\begin{matrix}0&0\\{\vdots}&{\vdots}\end{matrix}&\begin{matrix}0&0\\{\vdots}&{\vdots}\end{matrix}&\begin{matrix}1&{\dots}\\{\vdots}&{\ddots}\end{matrix}\end{matrix}\right) \end{equation*}\] Beweis:
Die p-Reihe von Matrix A wird mit n-Spalte von Matrix B multipliziert.
F"ur n=p gilt:
\[\begin{equation*} \left(\genfrac{}{}{0pt}{0}p0\right)\ast \left(\genfrac{}{}{0pt}{0}n0\right)=\left(\genfrac{}{}{0pt}{0}p0\right)\ast \left(\genfrac{}{}{0pt}{0}p0\right)=1 \end{equation*}\] F"ur p=n-1 gilt:
\[\begin{equation*} -\left(\genfrac{}{}{0pt}{0}p1\right)\ast \left(\genfrac{}{}{0pt}{0}{p-1}0\right)+\left(\genfrac{}{}{0pt}{0}p0\right)\ast \left(\genfrac{}{}{0pt}{0}p0\right) \end{equation*}\] F"ur p=n-2 gilt:
\[\begin{equation*} \left(\genfrac{}{}{0pt}{0}p2\right)\ast \left(\genfrac{}{}{0pt}{0}{p-2}0\right)-\left(\genfrac{}{}{0pt}{0}p1\right)\ast \left(\genfrac{}{}{0pt}{0}{p-1}1\right)+\left(\genfrac{}{}{0pt}{0}p0\right)\ast \left(\genfrac{}{}{0pt}{0}p2\right) \end{equation*}\] F"ur p\(\textgreater\)n gilt:
\[\begin{equation*} \left(\genfrac{}{}{0pt}{0}pn\right)\ast \left(\genfrac{}{}{0pt}{0}{p-n}0\right)-\left(\genfrac{}{}{0pt}{0}p{n-1}\right)\ast \left(\genfrac{}{}{0pt}{0}{p-n+1}1\right)+\left(\genfrac{}{}{0pt}{0}p{n-2}\right)\ast \left(\genfrac{}{}{0pt}{0}{p-n+2}2\right)-{\dots}-\left(\genfrac{}{}{0pt}{0}p1\right)\ast \left(\genfrac{}{}{0pt}{0}{p-1}{n-1}\right)+\left(\genfrac{}{}{0pt}{0}p0\right)\ast \left(\genfrac{}{}{0pt}{0}pn\right) \end{equation*}\] Oder auch
\[\begin{equation*} -\left(\genfrac{}{}{0pt}{0}pn\right)\ast \left(\genfrac{}{}{0pt}{0}{p-n}0\right)+\left(\genfrac{}{}{0pt}{0}p{n-1}\right)\ast \left(\genfrac{}{}{0pt}{0}{p-n+1}1\right)-{\dots}-\left(\genfrac{}{}{0pt}{0}p1\right)\ast \left(\genfrac{}{}{0pt}{0}{p-1}{n-1}\right)+\left(\genfrac{}{}{0pt}{0}p0\right)\ast \left(\genfrac{}{}{0pt}{0}pn\right) \end{equation*}\] Des weiteren seien die folgenden Werte gegeben und werden wie folgt abgebildet:
\[\begin{equation*} x_1x_2x_3x_4x_5x_6{\dots}x_{z-1} \end{equation*}\] \[\begin{equation*} y_1y_2y_3y_4y_5y_6y_7{\dots}y_z \end{equation*}\] Hierf"ur soll gelten:
\[\begin{equation*} x_n-x_{n+1}=y_{n+1} \end{equation*}\] \[\begin{equation*} x_{n-1}-x_n=y_n \end{equation*}\] Wobei f"ur die \(y_1\) gilt: \(y_1=-x_1\) und \(y_z=x_{z-1}\)
Dadurch wird jeder Wert \(x_n\) einmal positiv als auch negativ abgebildet. Somit gilt: \(\sum _{n=1}^zy_n=0\)
Dies gilt auch bei den Zusammenhang von \(a\ast x_n-a\ast x_{n+1}=y_{n+1}\)
Die Matrixmultiplikation von A und B wird wie folgt betrachtet:
\[\begin{equation*} -\left(\genfrac{}{}{0pt}{0}pn\right)\ast \left(\genfrac{}{}{0pt}{0}{p-n}0\right)+{\dots}+\left(\genfrac{}{}{0pt}{0}p{n-s}\right)\ast \left(\genfrac{}{}{0pt}{0}{p-n+s}s\right)-\left(\genfrac{}{}{0pt}{0}p{n-s+1}\right)\ast \left(\genfrac{}{}{0pt}{0}{p-n+s+1}{s+1}\right){\dots}+\left(\genfrac{}{}{0pt}{0}p0\right)\ast \left(\genfrac{}{}{0pt}{0}pn\right) \end{equation*}\] [Warning: Draw object ignored]Nächste Reihe:
\[\begin{equation*} \left(\genfrac{}{}{0pt}{0}p{n+1}\right)\ast \left(\genfrac{}{}{0pt}{0}{p-n+1}0\right)+{\dots}+\left(\genfrac{}{}{0pt}{0}p{n-s}\right)\ast \left(\genfrac{}{}{0pt}{0}{p-n+s+1}{s+1}\right)-{\dots}+\left(\genfrac{}{}{0pt}{0}p0\right)\ast \left(\genfrac{}{}{0pt}{0}p{n+1}\right) \end{equation*}\] \[\begin{equation*} n+1-(s+1) \end{equation*}\] Mit dem Ansatz \(a\ast x_n-a\ast x_{n+1}=y_{n+1}\) soll nun gelten:
\[\begin{equation*} a\ast \left(\genfrac{}{}{0pt}{0}p{n-s}\right)\ast \left(\genfrac{}{}{0pt}{0}{p-n+s}s\right)+a\ast \left(\genfrac{}{}{0pt}{0}p{n-s+1}\right)\ast \left(\genfrac{}{}{0pt}{0}{p-n+s+1}{s+1}\right)=\left(\genfrac{}{}{0pt}{0}p{n-s}\right)\ast \left(\genfrac{}{}{0pt}{0}{p-n+s+1}{s+1}\right) \end{equation*}\] \[\begin{equation*} \frac{\frac{a\ast p!}{\left(n-s\right)!\left(p-n+s\right)!}\ast \left(p-n+s\right)!}{s!\left(p-n\right)!}+\frac{\frac{a\ast p!}{\left(n-s-1\right)!\left(p-n+s+1\right)!}\ast \left(p-n+s+1\right)!}{\left(s+1\right)!\left(p-n\right)!}=? \end{equation*}\] \[\begin{equation*} =\frac{\frac{p!}{\left(n-s\right)!\left(p-n+s\right)!}\ast \left(p-n+s\right)!}{\left(s+1\right)!\left(p-n-1\right)!} \end{equation*}\] \[\begin{equation*} \frac{a\ast p!}{\left(n-s\right)!s!\left(p-n\right)!}+\frac{a\ast p!}{\left(n-s-1\right)!\left(s+1\right)!\left(p-n\right)!}=\frac{p!}{\left(n-s\right)!\left(s+1\right)!\left(p-n-1\right)!} \end{equation*}\] \[\begin{equation*} a\ast p!\ast \left(s+1\right)+a\ast p!\ast \left(n-s\right)=p!(p-n) \end{equation*}\] \[\begin{equation*} a\ast p!\left(s+1+n-s\right)=p!(p-n) \end{equation*}\] \[\begin{equation*} a=\frac{p-n}{n+1} \end{equation*}\] Damit ist \(a\left(p,n\right)\) unabhängig von \(s\) und da p und n f"ur eine bestimmte Reihe und Spalte konstant ist gilt:
\[\begin{equation*} \left(\genfrac{}{}{0pt}{0}p{n+1}\right)\ast \left(\genfrac{}{}{0pt}{0}{p-n+1}0\right)+{\dots}+\left(\genfrac{}{}{0pt}{0}p{n-s}\right)\ast \left(\genfrac{}{}{0pt}{0}{p-n+s+1}{s+1}\right)-{\dots}+\left(\genfrac{}{}{0pt}{0}p0\right)\ast \left(\genfrac{}{}{0pt}{0}p{n+1}\right)=0 \end{equation*}\] Werte p{}n sind ebenfalls 0, da jeder Wert mit 0 multipliziert wird.
Somit gilt: \(p=n\rightarrow 1\)
\[\begin{equation*} p<n\rightarrow 0 \end{equation*}\] \[\begin{equation*} p>n\rightarrow 0 \end{equation*}\] Damit ergibt sich aus A*B:
\[\begin{equation*} A\ast B=\left(\begin{matrix}\begin{matrix}1&0\\0&1\end{matrix}&\begin{matrix}0&0\\0&0\end{matrix}&\begin{matrix}0&{\dots}\\0&{\dots}\end{matrix}\\\begin{matrix}0&0\\0&0\end{matrix}&\begin{matrix}1&0\\0&1\end{matrix}&\begin{matrix}0&{\dots}\\0&{\dots}\end{matrix}\\\begin{matrix}0&0\\{\vdots}&{\vdots}\end{matrix}&\begin{matrix}0&0\\{\vdots}&{\vdots}\end{matrix}&\begin{matrix}1&{\dots}\\{\vdots}&{\ddots}\end{matrix}\end{matrix}\right) \ # Appendix \begin{equation*} A=\left(\begin{matrix}\begin{matrix}\left(\genfrac{}{}{0pt}{0}00\right)&0\\-\left(\genfrac{}{}{0pt}{0}11\right)&\left(\genfrac{}{}{0pt}{0}10\right)\end{matrix}&\begin{matrix}0&0\\0&0\end{matrix}&\begin{matrix}0&{\dots}\\0&{\dots}\end{matrix}\\\begin{matrix}\left(\genfrac{}{}{0pt}{0}22\right)&-\left(\genfrac{}{}{0pt}{0}21\right)\\-\left(\genfrac{}{}{0pt}{0}33\right)&\left(\genfrac{}{}{0pt}{0}32\right)\end{matrix}&\begin{matrix}\left(\genfrac{}{}{0pt}{0}20\right)&0\\-\left(\genfrac{}{}{0pt}{0}31\right)&\left(\genfrac{}{}{0pt}{0}30\right)\end{matrix}&\begin{matrix}0&{\dots}\\0&{\dots}\end{matrix}\\\begin{matrix}\left(\genfrac{}{}{0pt}{0}44\right)&-\left(\genfrac{}{}{0pt}{0}43\right)\\{\vdots}&{\vdots}\end{matrix}&\begin{matrix}\left(\genfrac{}{}{0pt}{0}42\right)&-\left(\genfrac{}{}{0pt}{0}41\right)\\{\vdots}&{\vdots}\end{matrix}&\begin{matrix}\left(\genfrac{}{}{0pt}{0}40\right)&{\dots}\\{\vdots}&{\ddots}\end{matrix}\end{matrix}\right) \end{equation*}\] \[\begin{equation*} B=\left(\begin{matrix}\begin{matrix}\left(\genfrac{}{}{0pt}{0}00\right)&0\\\left(\genfrac{}{}{0pt}{0}11\right)&\left(\genfrac{}{}{0pt}{0}10\right)\end{matrix}&\begin{matrix}0&0\\0&0\end{matrix}&\begin{matrix}0&{\dots}\\0&{\dots}\end{matrix}\\\begin{matrix}\left(\genfrac{}{}{0pt}{0}22\right)&\left(\genfrac{}{}{0pt}{0}21\right)\\\left(\genfrac{}{}{0pt}{0}33\right)&\left(\genfrac{}{}{0pt}{0}32\right)\end{matrix}&\begin{matrix}\left(\genfrac{}{}{0pt}{0}20\right)&0\\\left(\genfrac{}{}{0pt}{0}31\right)&\left(\genfrac{}{}{0pt}{0}30\right)\end{matrix}&\begin{matrix}0&{\dots}\\0&{\dots}\end{matrix}\\\begin{matrix}\left(\genfrac{}{}{0pt}{0}44\right)&\left(\genfrac{}{}{0pt}{0}43\right)\\{\vdots}&{\vdots}\end{matrix}&\begin{matrix}\left(\genfrac{}{}{0pt}{0}42\right)&\left(\genfrac{}{}{0pt}{0}41\right)\\{\vdots}&{\vdots}\end{matrix}&\begin{matrix}\left(\genfrac{}{}{0pt}{0}40\right)&{\dots}\\{\vdots}&{\ddots}\end{matrix}\end{matrix}\right) \end{equation*}\] \[\begin{equation*} A\ast B=\left(\begin{matrix}\begin{matrix}1&0\\0&1\end{matrix}&\begin{matrix}0&0\\0&0\end{matrix}&\begin{matrix}0&{\dots}\\0&{\dots}\end{matrix}\\\begin{matrix}0&0\\0&0\end{matrix}&\begin{matrix}1&0\\0&1\end{matrix}&\begin{matrix}0&{\dots}\\0&{\dots}\end{matrix}\\\begin{matrix}0&0\\{\vdots}&{\vdots}\end{matrix}&\begin{matrix}0&0\\{\vdots}&{\vdots}\end{matrix}&\begin{matrix}1&{\dots}\\{\vdots}&{\ddots}\end{matrix}\end{matrix}\right) \end{equation*}\] Die p-Reihe von Matrix A wird mit n-Spalte von Matrix B multipliziert.
Für n=p gilt:
\[\begin{equation*} \left(\genfrac{}{}{0pt}{0}p0\right)\ast \left(\genfrac{}{}{0pt}{0}n0\right)=\left(\genfrac{}{}{0pt}{0}p0\right)\ast \left(\genfrac{}{}{0pt}{0}p0\right)=1 \end{equation*}\] Für p=n-1 gilt:
\[\begin{equation*} -\left(\genfrac{}{}{0pt}{0}p1\right)\ast \left(\genfrac{}{}{0pt}{0}{p-1}0\right)+\left(\genfrac{}{}{0pt}{0}p0\right)\ast \left(\genfrac{}{}{0pt}{0}p0\right) \end{equation*}\] Für p=n-2 gilt:
\[\begin{equation*} \left(\genfrac{}{}{0pt}{0}p2\right)\ast \left(\genfrac{}{}{0pt}{0}{p-2}0\right)-\left(\genfrac{}{}{0pt}{0}p1\right)\ast \left(\genfrac{}{}{0pt}{0}{p-1}1\right)+\left(\genfrac{}{}{0pt}{0}p0\right)\ast \left(\genfrac{}{}{0pt}{0}p2\right) \end{equation*}\] Für p{}n gilt:
\[\begin{equation*} \left(\genfrac{}{}{0pt}{0}pn\right)\ast \left(\genfrac{}{}{0pt}{0}{p-n}0\right)-\left(\genfrac{}{}{0pt}{0}p{n-1}\right)\ast \left(\genfrac{}{}{0pt}{0}{p-n+1}1\right)+\left(\genfrac{}{}{0pt}{0}p{n-2}\right)\ast \left(\genfrac{}{}{0pt}{0}{p-n+2}2\right)-{\dots}-\left(\genfrac{}{}{0pt}{0}p1\right)\ast \left(\genfrac{}{}{0pt}{0}{p-1}{n-1}\right)+\left(\genfrac{}{}{0pt}{0}p0\right)\ast \left(\genfrac{}{}{0pt}{0}pn\right) \end{equation*}\] Oder auch
\[\begin{equation*} -\left(\genfrac{}{}{0pt}{0}pn\right)\ast \left(\genfrac{}{}{0pt}{0}{p-n}0\right)+\left(\genfrac{}{}{0pt}{0}p{n-1}\right)\ast \left(\genfrac{}{}{0pt}{0}{p-n+1}1\right)-{\dots}-\left(\genfrac{}{}{0pt}{0}p1\right)\ast \left(\genfrac{}{}{0pt}{0}{p-1}{n-1}\right)+\left(\genfrac{}{}{0pt}{0}p0\right)\ast \left(\genfrac{}{}{0pt}{0}pn\right) \end{equation*}\] Des weiteren seien die folgenden Werte gegeben und werden wie folgt abgebildet:
\[\begin{equation*} x_1x_2x_3x_4x_5x_6{\dots}x_{z-1} \end{equation*}\] \[\begin{equation*} y_1y_2y_3y_4y_5y_6y_7{\dots}y_z \end{equation*}\] Hierfür soll gelten:
\[\begin{equation*} x_n-x_{n+1}=y_{n+1} \end{equation*}\] \[\begin{equation*} x_{n-1}-x_n=y_n \end{equation*}\] Wobei für die \(y_1\) gilt: \(y_1=-x_1\) und \(y_z=x_{z-1}\)
Dadurch wird jeder Wert \(x_n\) einmal positiv als auch negativ abgebildet. Somit gilt: \(\sum _{n=1}^zy_n=0\)
Dies gilt auch bei den Zusammenhang von \(a\ast x_n-a\ast x_{n+1}=y_{n+1}\)
Die Matrixmultiplikation von A und B wird wie folgt betrachtet:
\[\begin{equation*} -\left(\genfrac{}{}{0pt}{0}pn\right)\ast \left(\genfrac{}{}{0pt}{0}{p-n}0\right)+{\dots}+\left(\genfrac{}{}{0pt}{0}p{n-s}\right)\ast \left(\genfrac{}{}{0pt}{0}{p-n+s}s\right)-\left(\genfrac{}{}{0pt}{0}p{n-s+1}\right)\ast \left(\genfrac{}{}{0pt}{0}{p-n+s+1}{s+1}\right){\dots}+\left(\genfrac{}{}{0pt}{0}p0\right)\ast \left(\genfrac{}{}{0pt}{0}pn\right) \end{equation*}\] [Warning: Draw object ignored]Nächste Reihe:
\[\begin{equation*} \left(\genfrac{}{}{0pt}{0}p{n+1}\right)\ast \left(\genfrac{}{}{0pt}{0}{p-n+1}0\right)+{\dots}+\left(\genfrac{}{}{0pt}{0}p{n-s}\right)\ast \left(\genfrac{}{}{0pt}{0}{p-n+s+1}{s+1}\right)-{\dots}+\left(\genfrac{}{}{0pt}{0}p0\right)\ast \left(\genfrac{}{}{0pt}{0}p{n+1}\right) \end{equation*}\] \[\begin{equation*} n+1-(s+1) \end{equation*}\] Mit dem Ansatz \(a\ast x_n-a\ast x_{n+1}=y_{n+1}\) soll nun gelten:
\[\begin{equation*} a\ast \left(\genfrac{}{}{0pt}{0}p{n-s}\right)\ast \left(\genfrac{}{}{0pt}{0}{p-n+s}s\right)+a\ast \left(\genfrac{}{}{0pt}{0}p{n-s+1}\right)\ast \left(\genfrac{}{}{0pt}{0}{p-n+s+1}{s+1}\right)=\left(\genfrac{}{}{0pt}{0}p{n-s}\right)\ast \left(\genfrac{}{}{0pt}{0}{p-n+s+1}{s+1}\right) \end{equation*}\] \[\begin{equation*} \frac{\frac{a\ast p!}{\left(n-s\right)!\left(p-n+s\right)!}\ast \left(p-n+s\right)!}{s!\left(p-n\right)!}+\frac{\frac{a\ast p!}{\left(n-s-1\right)!\left(p-n+s+1\right)!}\ast \left(p-n+s+1\right)!}{\left(s+1\right)!\left(p-n\right)!}=? \end{equation*}\] \[\begin{equation*} =\frac{\frac{p!}{\left(n-s\right)!\left(p-n+s\right)!}\ast \left(p-n+s\right)!}{\left(s+1\right)!\left(p-n-1\right)!} \end{equation*}\] \[\begin{equation*} \frac{a\ast p!}{\left(n-s\right)!s!\left(p-n\right)!}+\frac{a\ast p!}{\left(n-s-1\right)!\left(s+1\right)!\left(p-n\right)!}=\frac{p!}{\left(n-s\right)!\left(s+1\right)!\left(p-n-1\right)!} \end{equation*}\] \[\begin{equation*} a\ast p!\ast \left(s+1\right)+a\ast p!\ast \left(n-s\right)=p!(p-n) \end{equation*}\] \[\begin{equation*} a\ast p!\left(s+1+n-s\right)=p!(p-n) \end{equation*}\] \[\begin{equation*} a=\frac{p-n}{n+1} \end{equation*}\] Damit ist \(a\left(p,n\right)\) unabhängig von \(s\) und da p und n für eine bestimmte Reihe und Spalte konstant ist gilt:
\[\begin{equation*} \left(\genfrac{}{}{0pt}{0}p{n+1}\right)\ast \left(\genfrac{}{}{0pt}{0}{p-n+1}0\right)+{\dots}+\left(\genfrac{}{}{0pt}{0}p{n-s}\right)\ast \left(\genfrac{}{}{0pt}{0}{p-n+s+1}{s+1}\right)-{\dots}+\left(\genfrac{}{}{0pt}{0}p0\right)\ast \left(\genfrac{}{}{0pt}{0}p{n+1}\right)=0 \end{equation*}\] Werte p{}n sind ebenfalls 0, da jeder Wert mit 0 multipliziert wird.
Somit gilt: \(p=n\rightarrow 1\)
\[\begin{equation*} p<n\rightarrow 0 \end{equation*}\] \[\begin{equation*} p>n\rightarrow 0 \end{equation*}\] Damit ergibt sich aus A*B:
\[\begin{equation*} A\ast B=\left(\begin{matrix}\begin{matrix}1&0\\0&1\end{matrix}&\begin{matrix}0&0\\0&0\end{matrix}&\begin{matrix}0&{\dots}\\0&{\dots}\end{matrix}\\\begin{matrix}0&0\\0&0\end{matrix}&\begin{matrix}1&0\\0&1\end{matrix}&\begin{matrix}0&{\dots}\\0&{\dots}\end{matrix}\\\begin{matrix}0&0\\{\vdots}&{\vdots}\end{matrix}&\begin{matrix}0&0\\{\vdots}&{\vdots}\end{matrix}&\begin{matrix}1&{\dots}\\{\vdots}&{\ddots}\end{matrix}\end{matrix}\right) \end{equation*}\]
7 What he actually sent me
knitr::include_graphics(
c("figures/jhcollatz3.png"))
knitr::include_graphics(
c("figures/jhcollatz4.png"))
knitr::include_graphics(
c("figures/jhcollatz5.png"))
knitr::include_graphics(
c("figures/jhcollatz6.png"))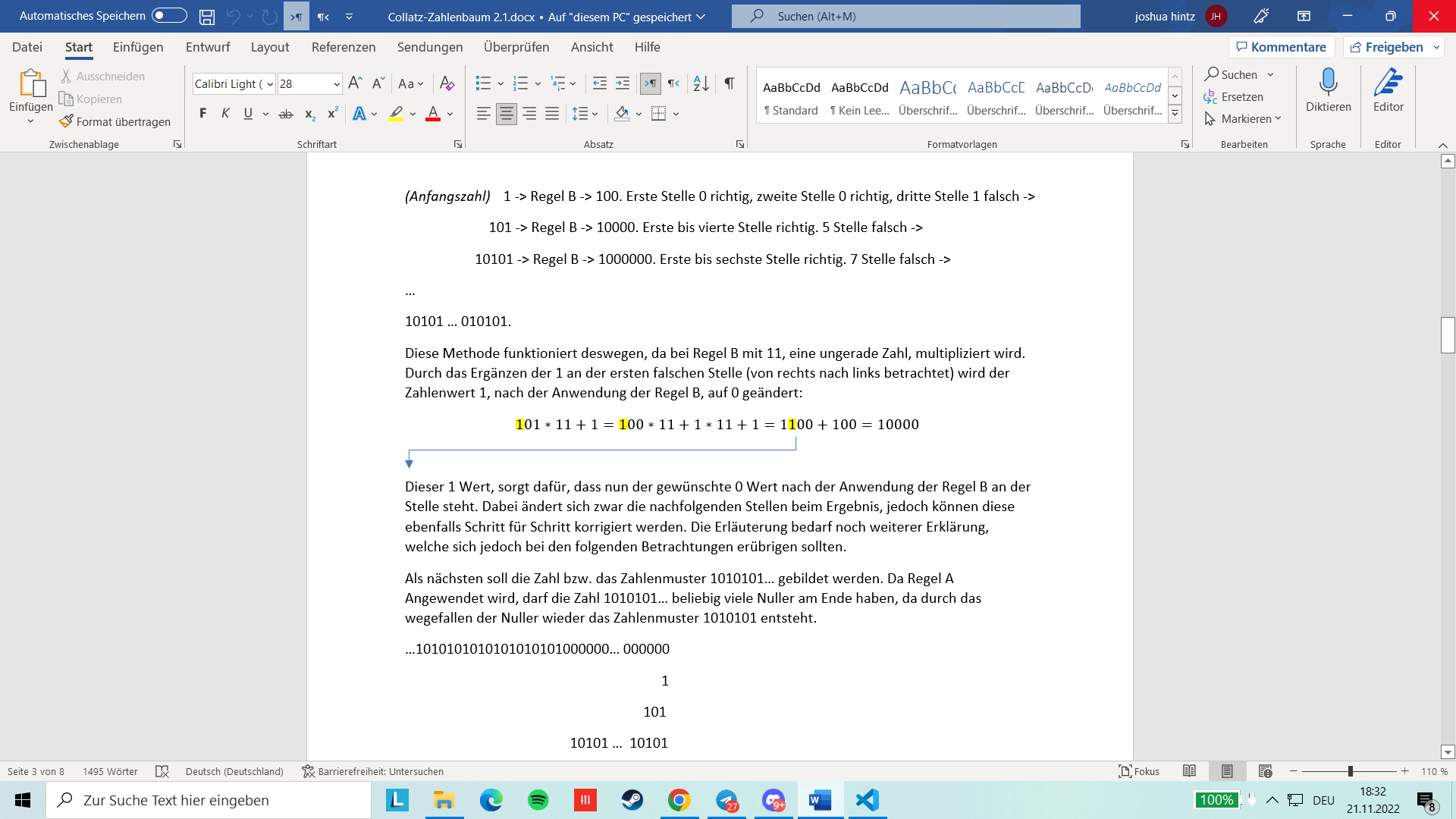
knitr::include_graphics(
c("figures/jhcollatz7.png"))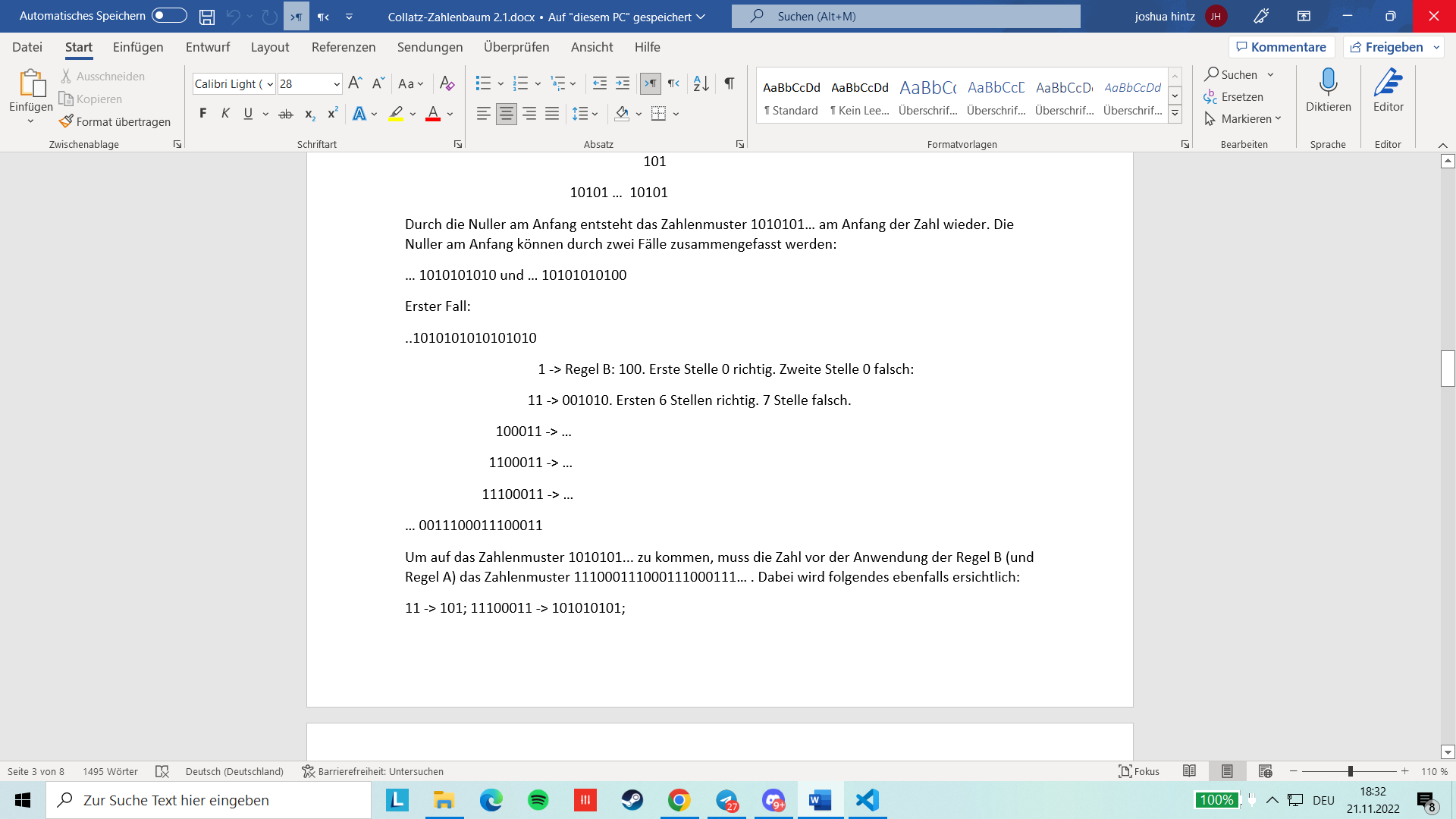
knitr::include_graphics(
c("figures/jhcollatz8.png"))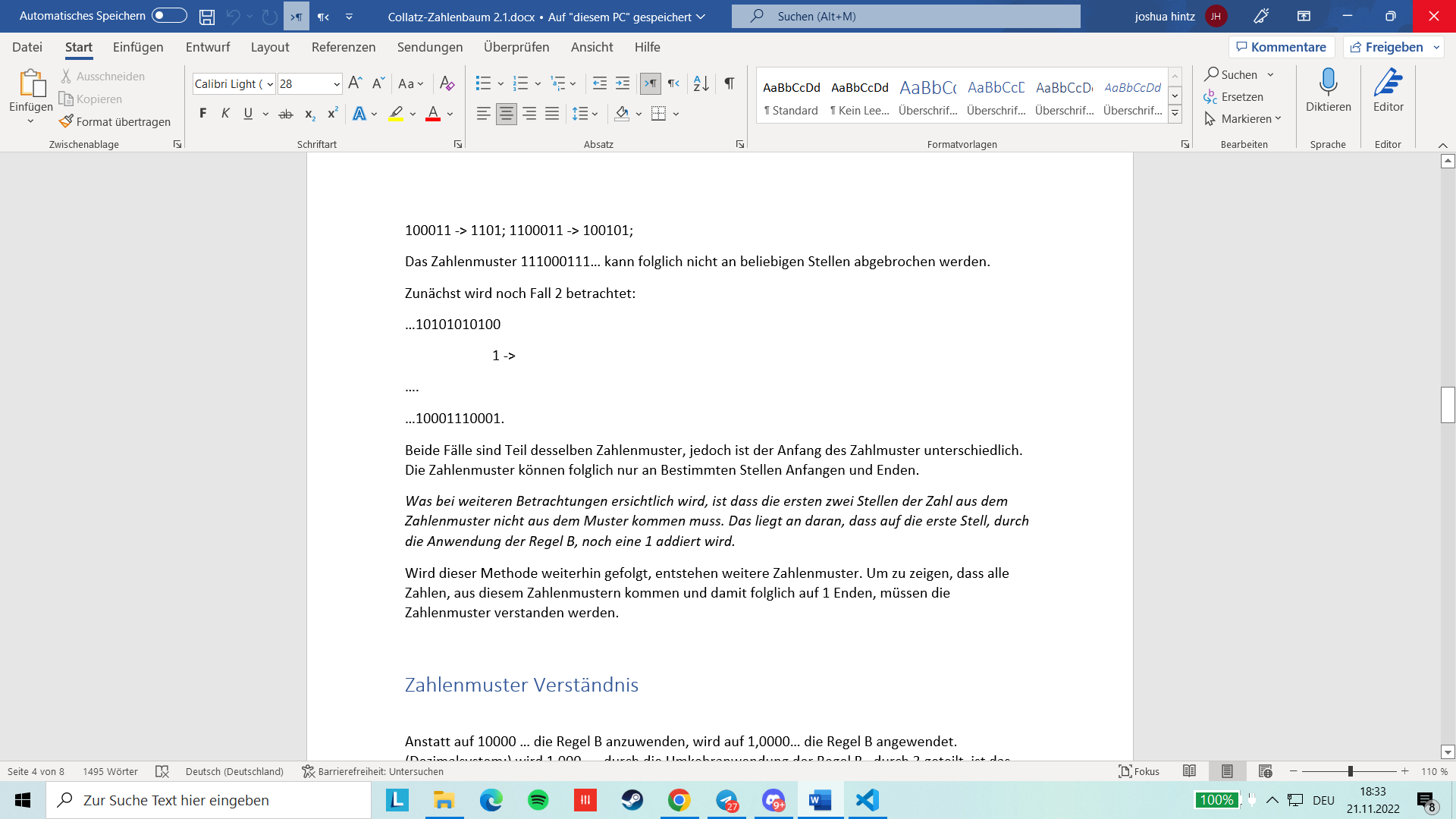
knitr::include_graphics(
c("figures/jhcollatz9.png"))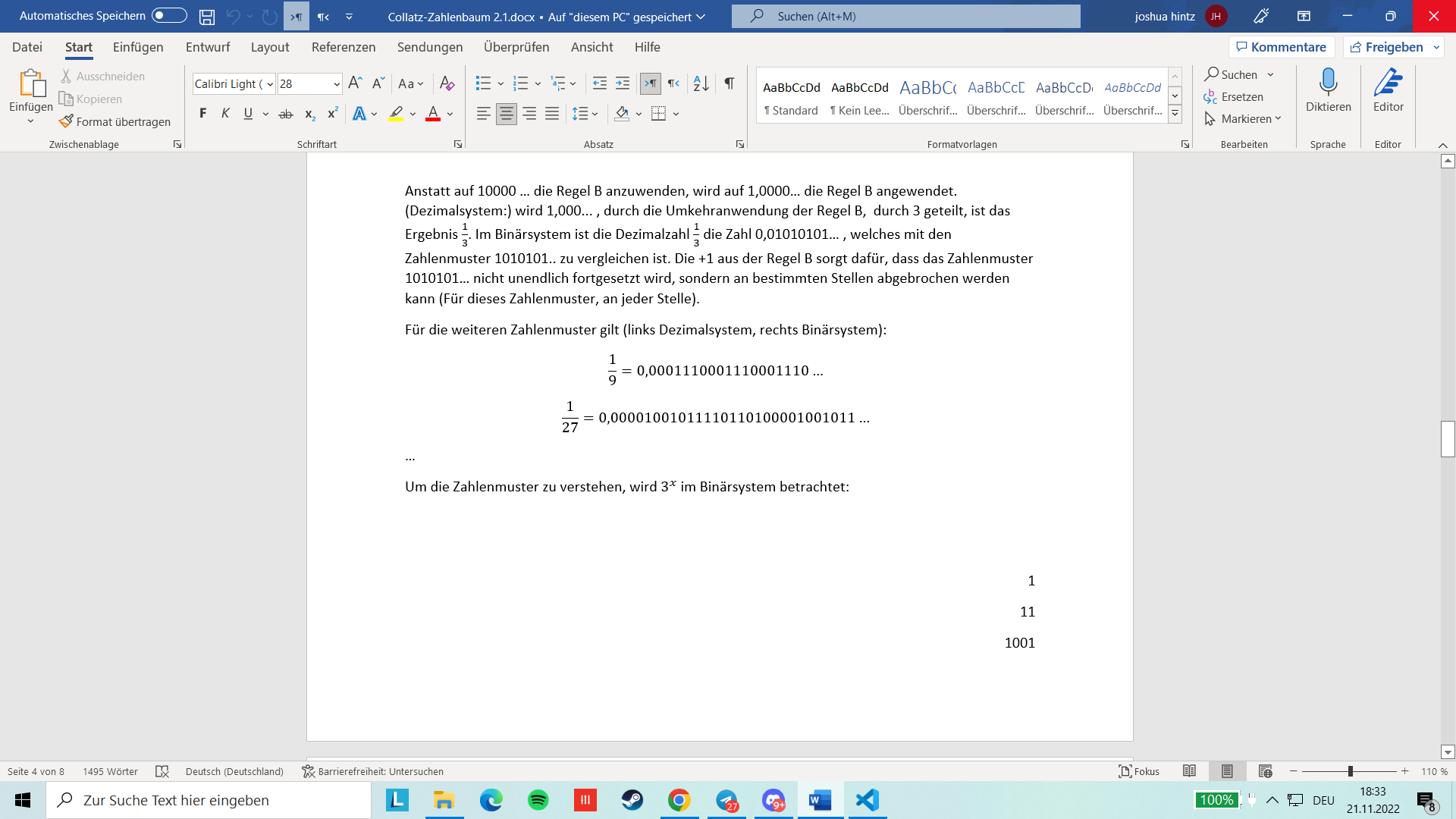
knitr::include_graphics(
c("figures/jhcollatz10.png"))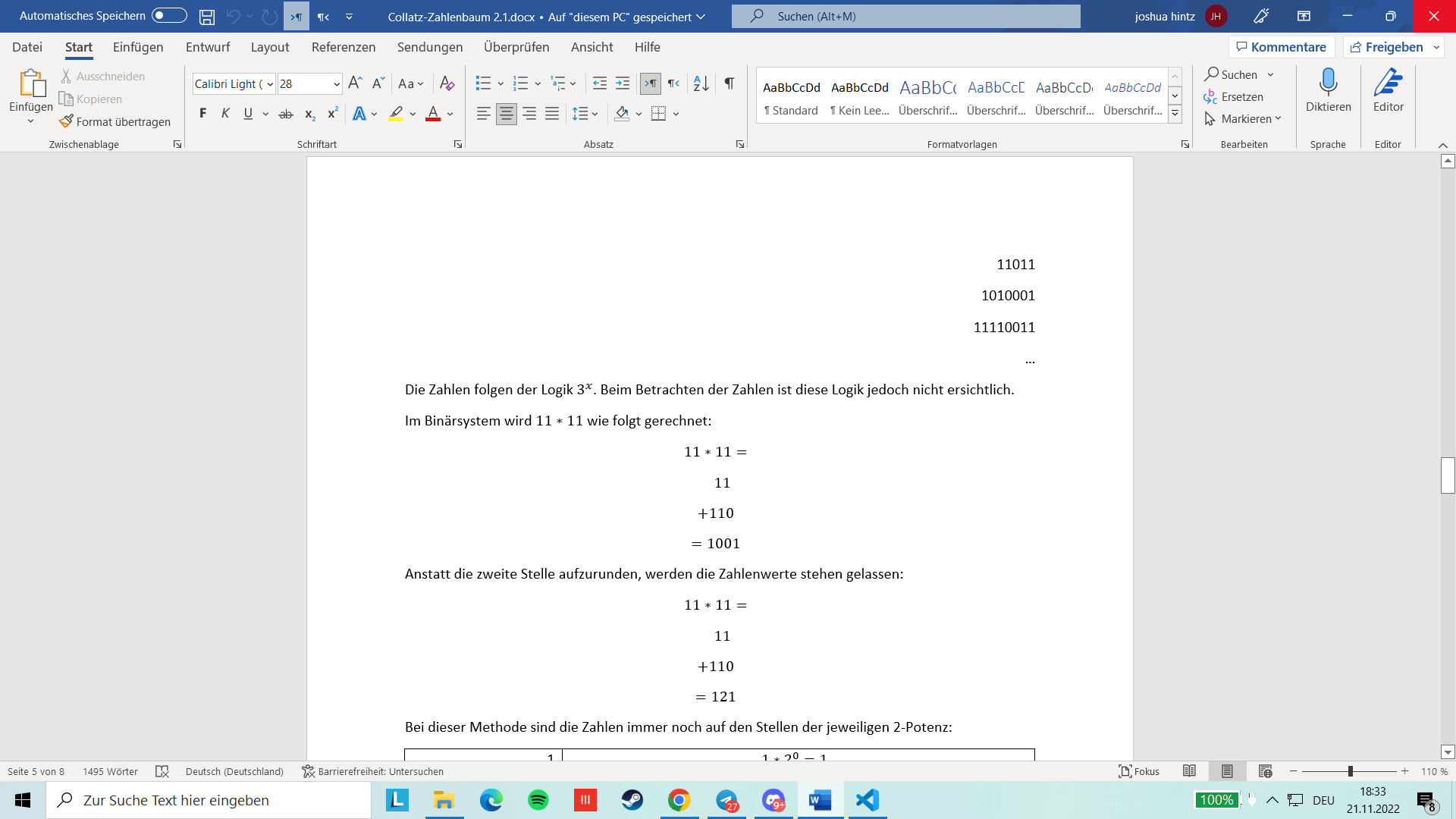
knitr::include_graphics(
c("figures/jhcollatz11.png"))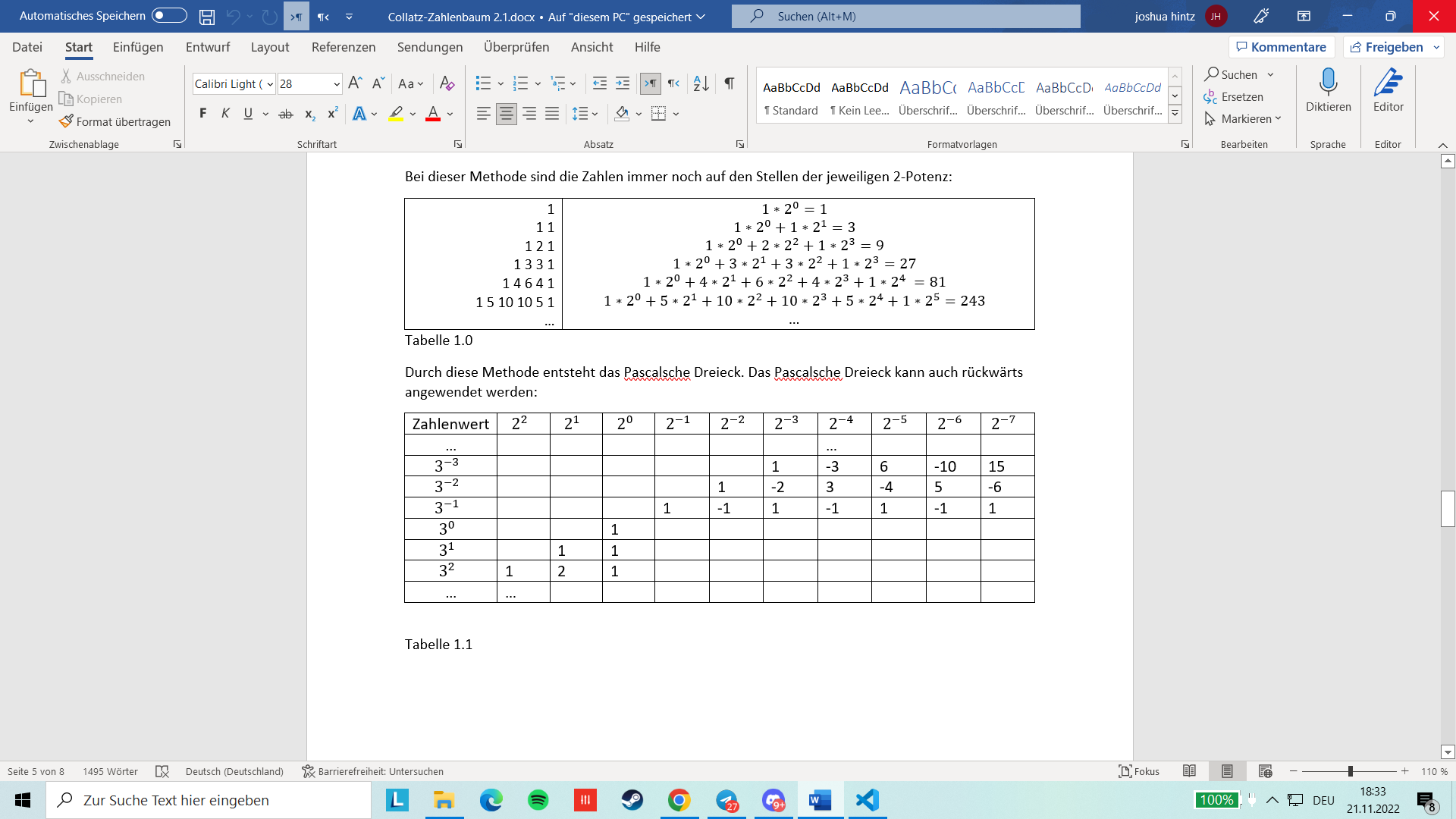
knitr::include_graphics(
c("figures/jhcollatz12.png"))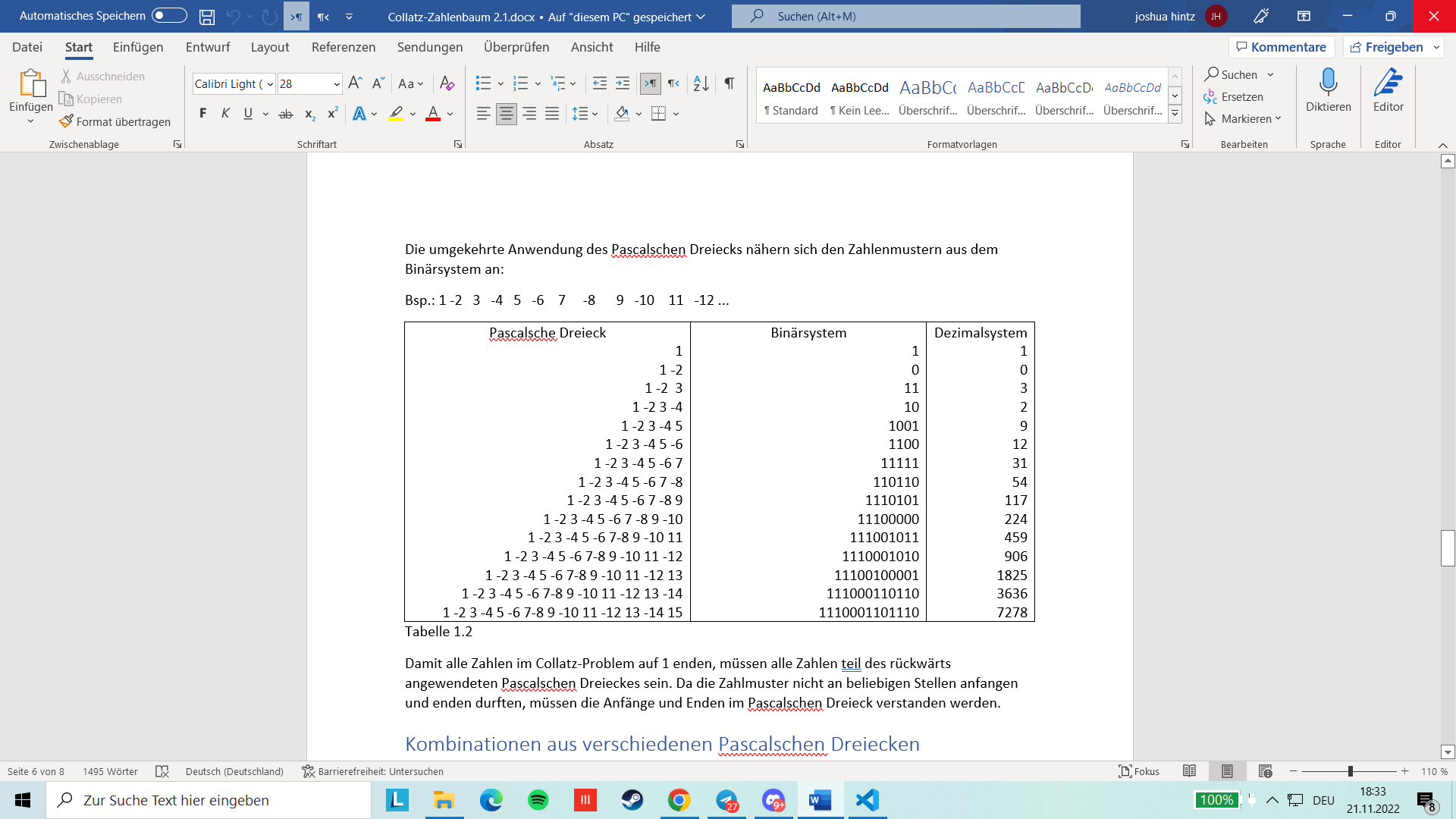
knitr::include_graphics(
c("figures/jhcollatz13.png"))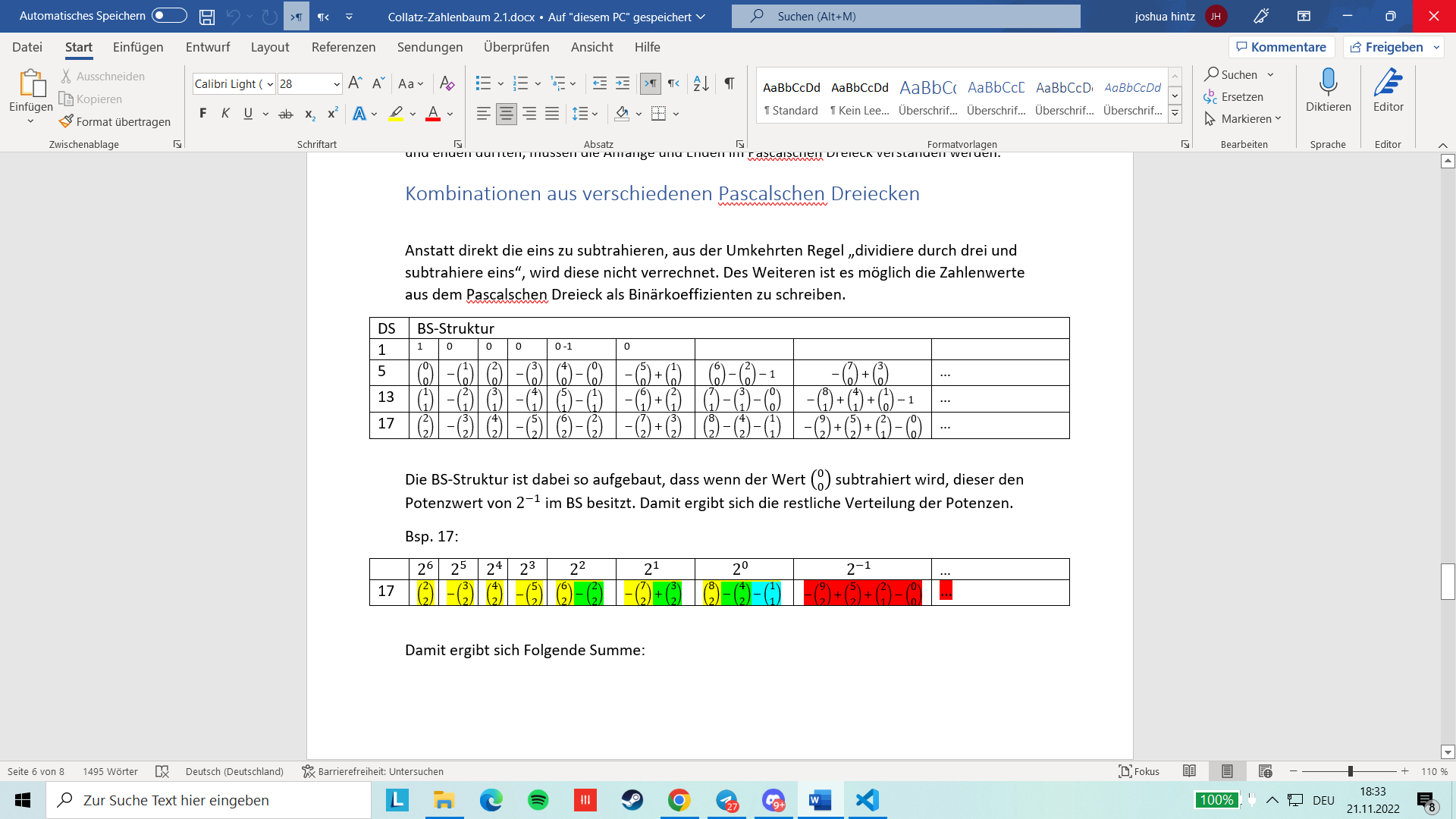
knitr::include_graphics(
c("figures/jhcollatz14.png"))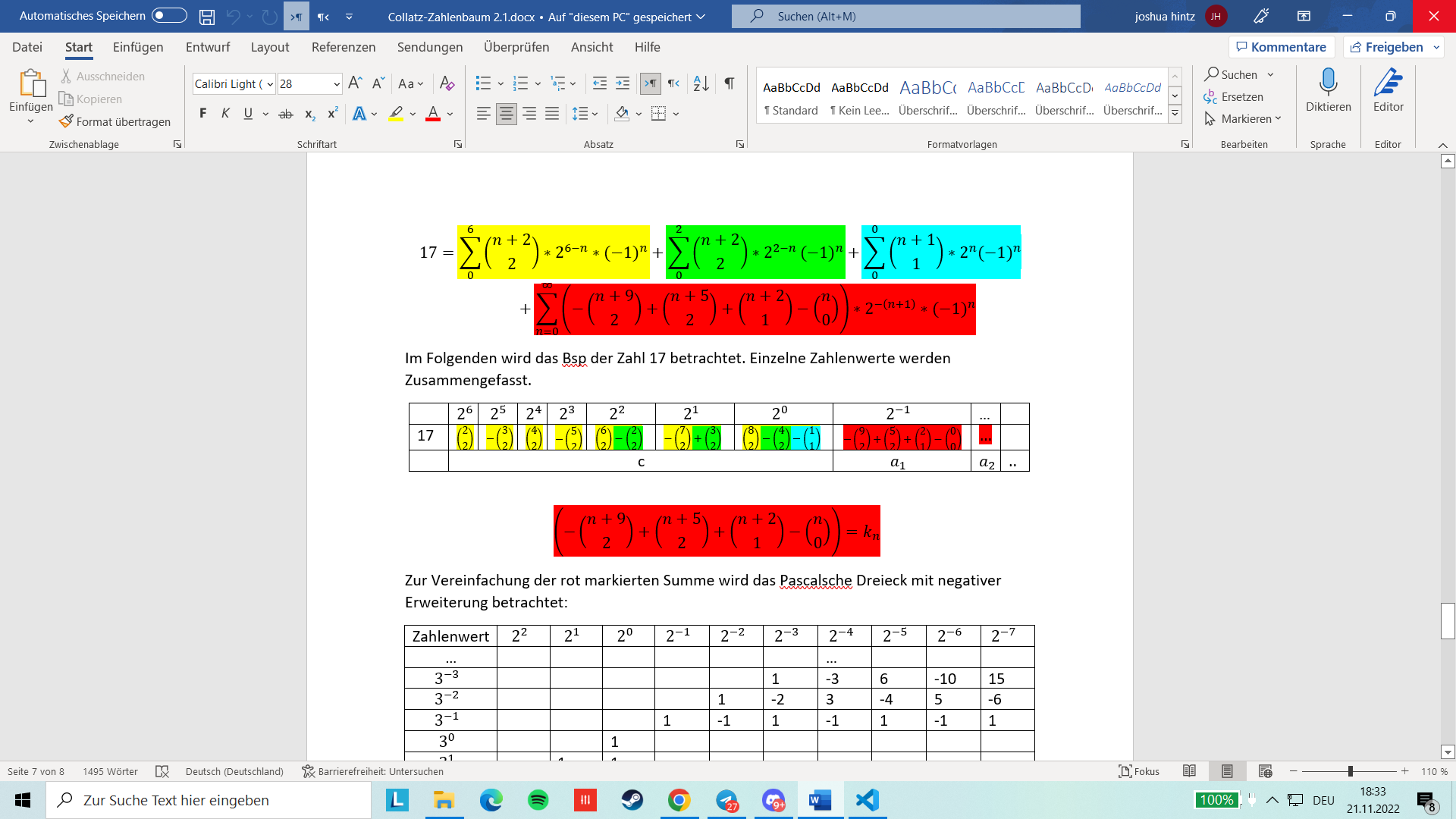
knitr::include_graphics(
c("figures/jhcollatz15.png"))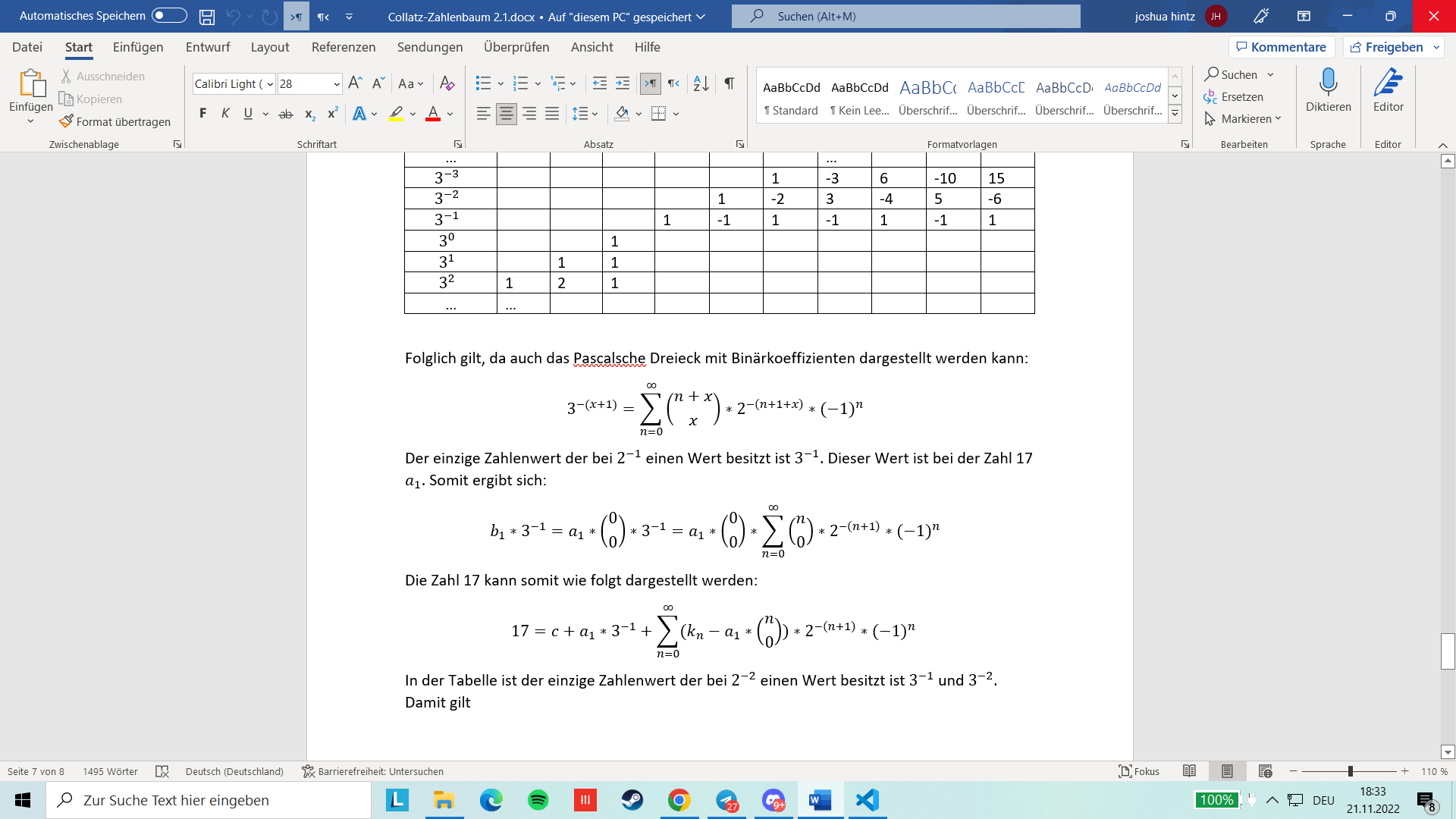
knitr::include_graphics(
c("figures/jhcollatz16.png"))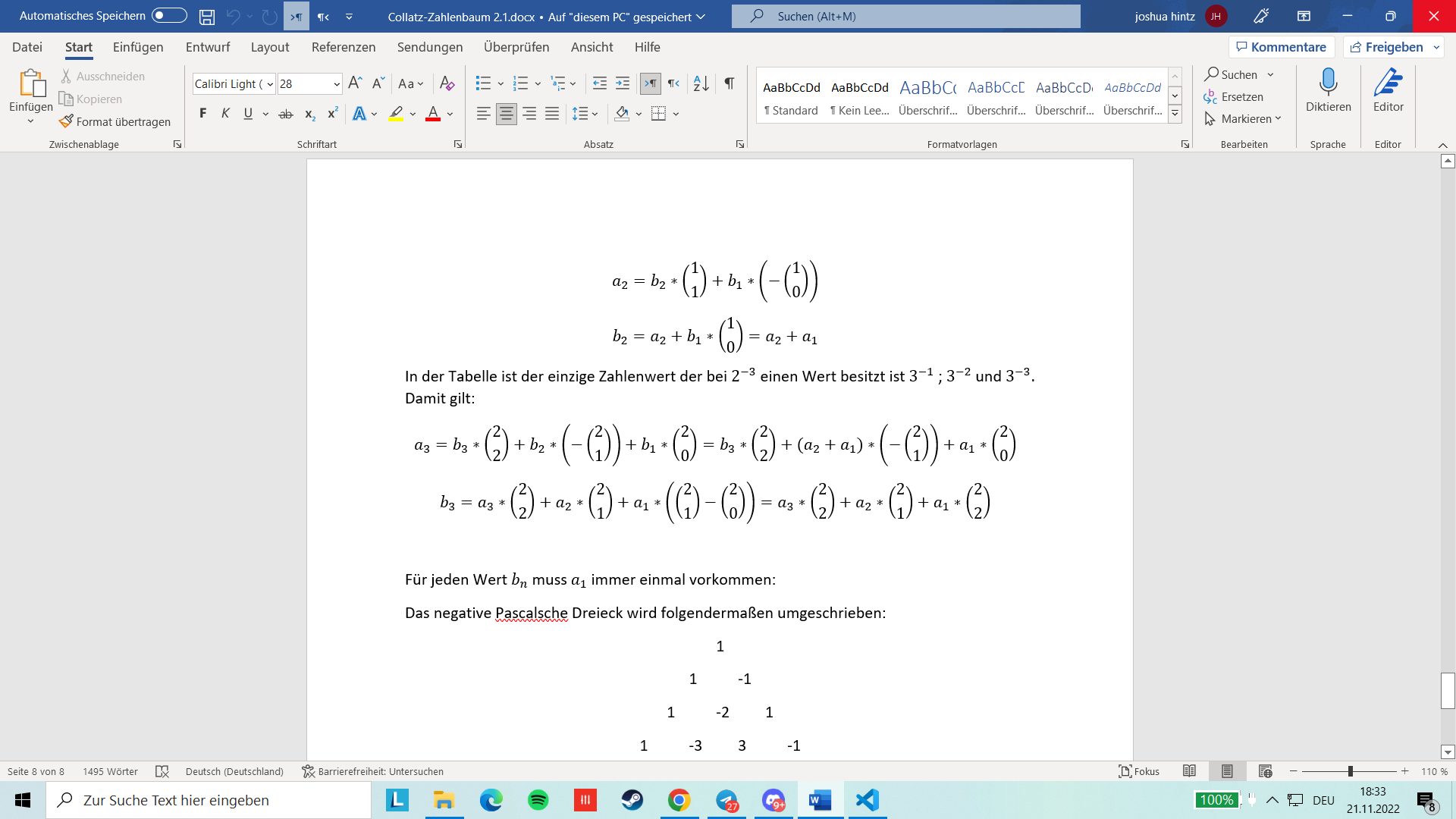
knitr::include_graphics(
c("figures/jhcollatz17.png")
)